Research Table of Contents
- Paper 1 (04/2017): Making simulations of planet-induced vortices more realistic.
- Paper 2 (01/2019): Connecting these simulations of planet-induced vortices to observations.
- Paper 3 (07/2021): Exploring how to extend vortex lifetimes even with realistic planet growth.
- Paper 4 (10/2023): Forming compact and other vortices that survive indefinitely.
- For the public.
Exploring how to extend vortex lifetimes even with realistic planet growth.
MNRAS paper (07/2021): Which planets trigger longer-lived vortices: low-mass or high-mass?
Five Years After HL Tau presentation: HL_Tau.pptx, PDF Version, YouTube Video, (Conference website here)
ITA Planet Formation Group Seminar presentation: Heidelberg.pptx, PDF Version, (Seminar website here)
One of the key results of our first paper was that realistic planet growth times drastically shorten vortex lifetimes; however, we only tested out planets more massive than Jupiter and disks with one specific scale height. Which planets trigger longer-lived vortices: low-mass or high-mass? Naively, you might think more massive planets create sharper bumps, which should lead to stronger longer-lived vortices, right? Well, it's not that simple.
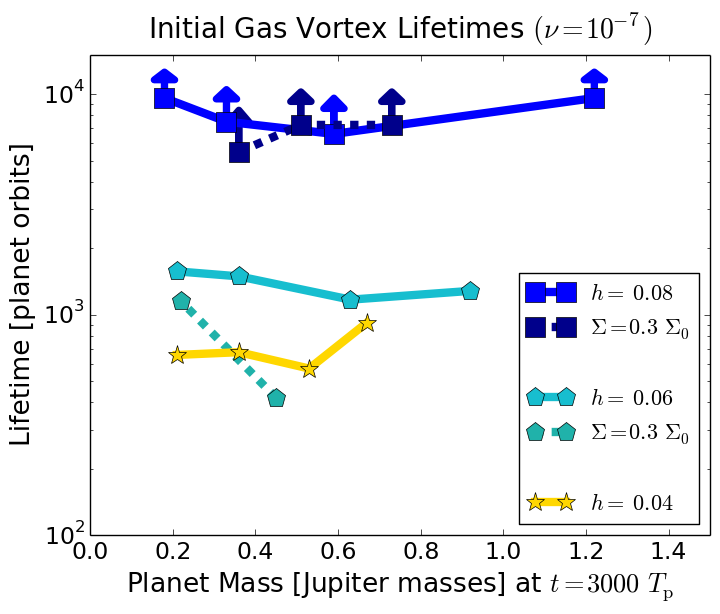
Right: The lifetimes of the initial vortices based on the gas in the low viscosity cases, as a function of two parameters: planet mass and disc mass. With a high disc mass, the initial vortex lifetime only depends on scale height, not planet mass.
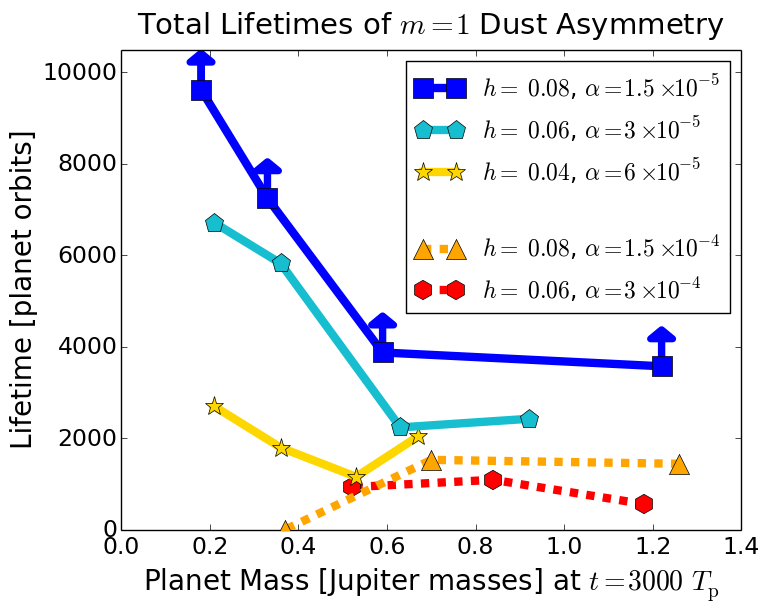
Above, you can see that the total vortex lifetimes are longer for lower-mass planets, even though the lifetimes of the initial vortices do not depend on the planet mass. What is going on? These patterns occur for a few separate reasons. First, in the low viscosity cases, shocks are responsible for killing each vortex. The strength of the shocks increases with higher Mach numbers, hence vortices in discs with low scale height decay much faster while vortices in discs with very high scale heights seemingly never decay.
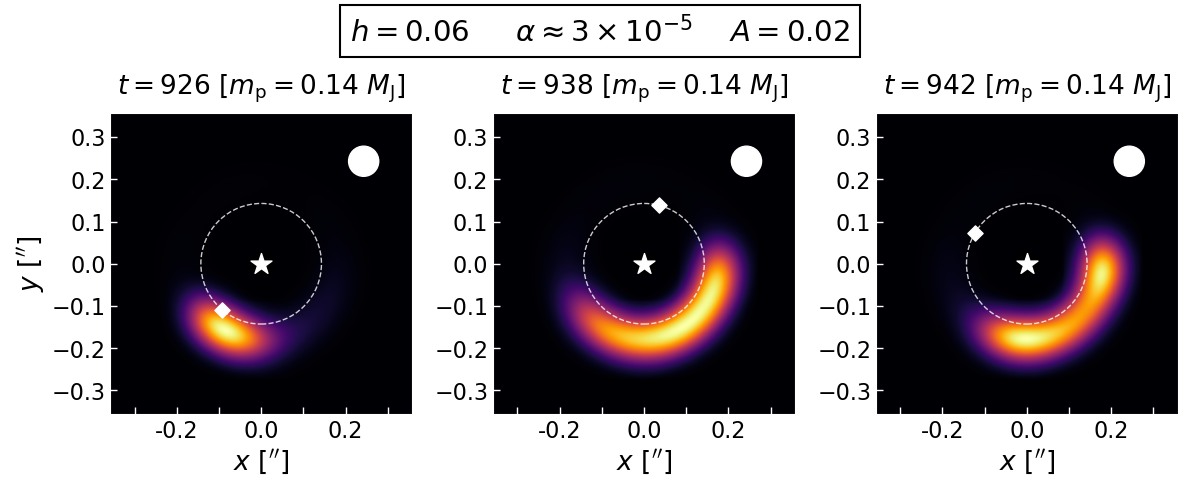
Yet, some of the total lifetimes in the low scale height cases are longer than others. Why? With lower-mass planets, the vortex can re-form, as you can see below with a sub-Saturn-mass planet!
As the density movie shows, the vortex re-forms three times (at t = 2600, 3150, and 3660 orbits). Although they may appear short-lived, the vortex is still alive at the end of this movie. Even though there is hardly any azimuthal contrast in the gas, there would still be a significant contrast in the dust from the point when the first vortex forms through the entire rest of the movie. Why do these vortices re-form? In order for a vortex to re-form, there must be a sharp bump in the crticial function shown in the radial profiles. Interestingly, after the initial vortex spreads into a ring, a new subtle bump in the critical function forms not at the pressure bump, but several scale heights inside the pressure bump. This subtle bump is able to trigger a new vortex at the pressure bump, but only because the separation isn't that large. If the planet were more massive, the subtle bump would be located in the same place while the pressure bump would be further away from the planet. As a result, a Jupiter-mass planet would not be able to re-trigger a vortex.
If you look at the vortex total dust lifetimes again though, the vortices in discs with large scale height also "live longer" with lower planet masses. The reason is an entirely different pathway shown below.
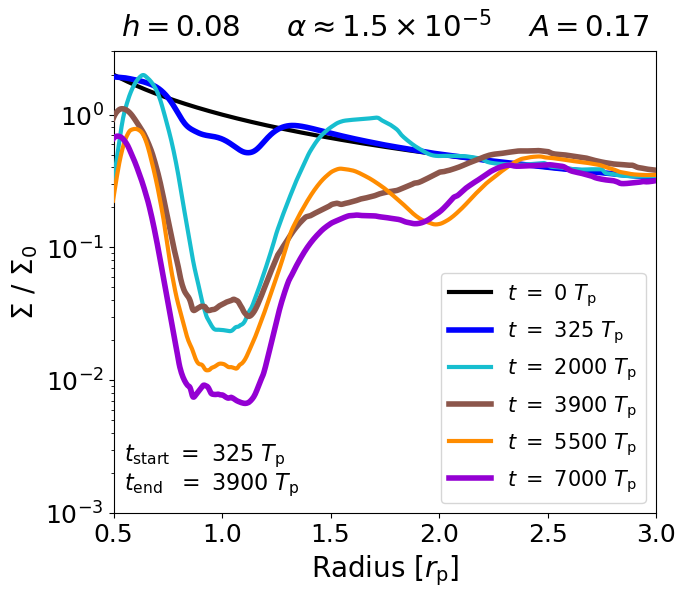
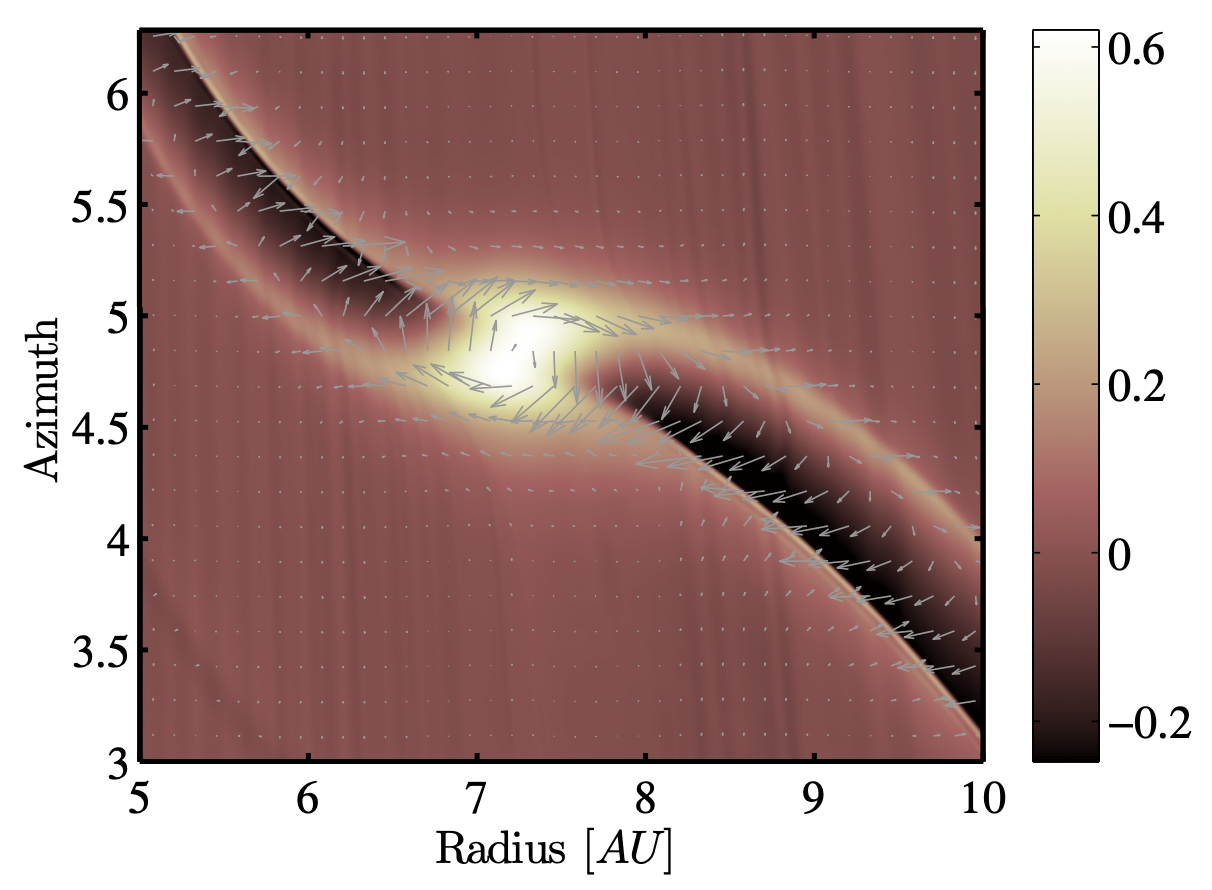
Right: Radial density profiles at key points. The initial vortex starts to migrate outwards once the initial pressure bump has been depleted by the vortex itself.
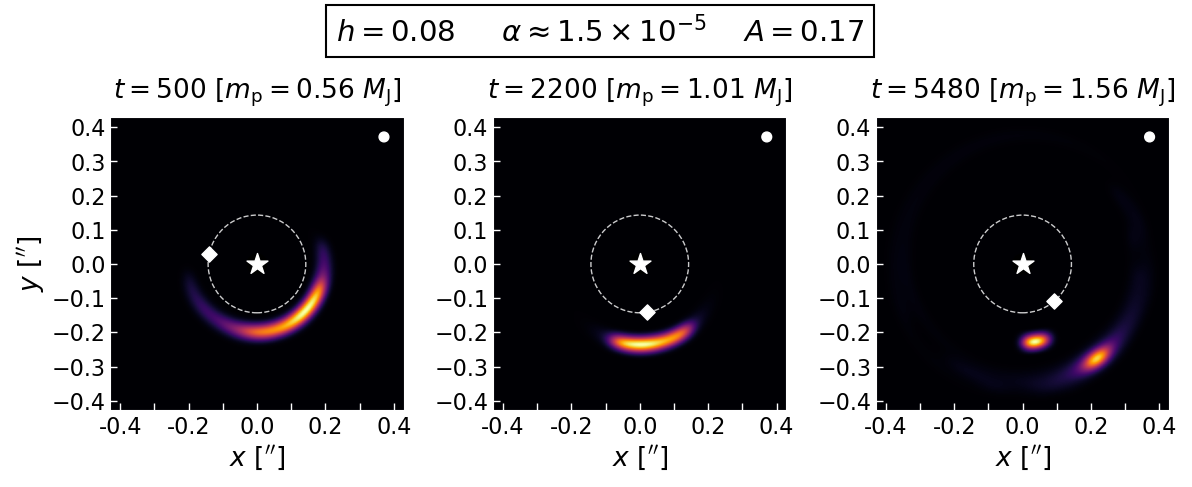
In the H/R = 0.08 cases with a high disc mass, the vortex never stops growing. Eventually, it grows enough to transition from elongated (minimum Rossby number > -0.15) to compact (minimum Rossby number < -0.15), where what separates these two states is the Rossby number of the vortex moreso than the extent. Furthermore, the compact vortex has much stronger spiral waves that can cause the vortex to lose angular momentum and shrink until the initial pressure bump depletes. After the pressure bump disappears, the vortex migrates outwards towards the new pressure bump. Meanwhile, a second vortex forms near the planet where a new bump in the critical function arose. This process happens much slower with less massive planets, allowing the initial vortex to stay where it formed for much longer (albeit, the initial vortex survives for at least 10000 orbits regardless of planet mass, just not near the planet).
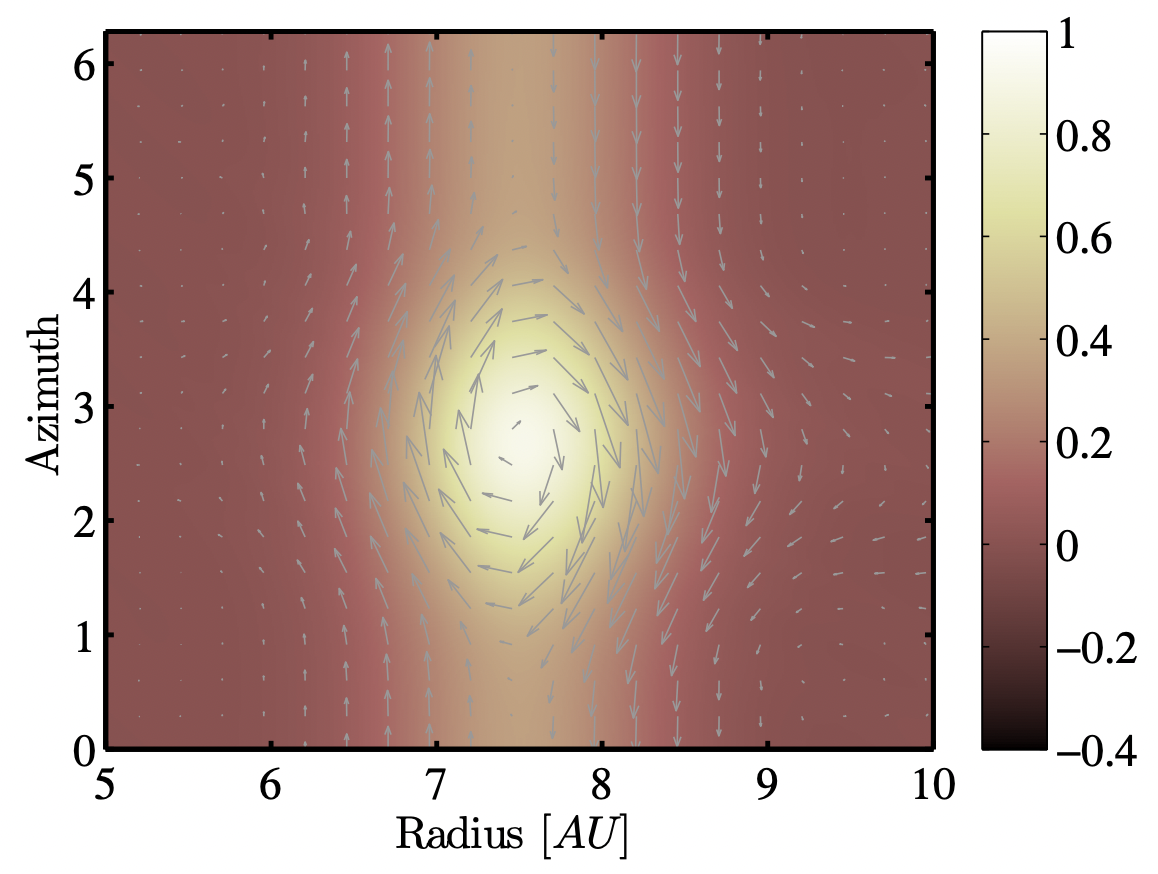
Models for the two types of vortices are shown below.
Now that we better understand how vortices can form and evolve, we went back to exploring what these vortices should look like in dust observations. Instead of just initializing the dust to a power-law profile, we applied an exponential cutoff so that the vortex wasn't constantly being fed with dust. This model better matches observations where crescent-shaped features are typically the outermost feature of a disk. We found that when cutting off the dust supply, the mm-sized dust can change shape from "elongated" to "compact" and back. It could also split into "double peaks" as it circulates through the vortex.
Moreover, the H/R = 0.08 cases with two vortices could potentially resemble disks like MWC 758.
Bonus: When re-triggering vortices, why does a new bump in the RWI critical function arise?
I'm glad you asked. The critical function is the surface density divided by the vorticity. Although the surface density does not change much after the planet opens a gap, the vorticity profile is still affected by the planet. Specifically, the planet shocks the disk with its spiral waves, thereby altering the vorticity profile continually. The pattern of the vorticity change is that it is positive close to the planet, and negative further away. The location where the vorticity change is most negative is close to the transition between a positive and a negative change, which happens just outside the horseshore region. As a result, the new bump in the RWI critical function forms just outside the horseshoe region. Because the width of the horseshoe region is not strongly dependent on planet mass, the location of the bump is not strongly dependent on planet mass either, even though the gap width increases with planet mass at a relatively higher rate.
Conference Talks
Five Years After HL Tau (December 2020)
AAS 237 Dissertation Talk (January 2021)
Contact Info
Find me in my office, or send me an email!